1.- Mentor Enciclopedia Temática Estudiantil Océano.
1.1.- Matemáticas - Primer Libro.
1.2.- Álgebra - Ecuaciones.
miércoles, 14 de noviembre de 2018
EXPLICACIÓN PRACTICA
APLICANDO LO APRENDIDO
Exponente Negativo
Factorizando
Aspa - Formula General
Fraccionaria
domingo, 11 de noviembre de 2018
ECUACIONES EXPONENCIALES RESUELTAS
EJEMPLO 1
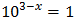
SOLUCIÓN:
Podemos escribir 1 como una potencia de 10:
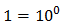
Con lo que podemos reescribir la ecuación como
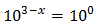
Por tanto, debe cumplirse
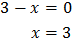
EJEMPLO 2
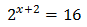
SOLUCIÓN:
Podemos reescribir la
ecuación de la siguiente manera:
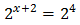
Por tanto, igualando
los exponentes:
X + 2 = 4
X = 4 - 2
Luego la solución de
la ecuación exponencial es:
X = 2
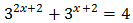
SOLUCIÓN:
Reescribimos los sumandos:
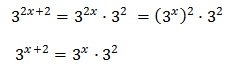
Con lo que podemos reescribir la ecuación como
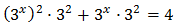
Sea el cambio de variable
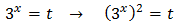
Sustituyendo en la ecuación obtenemos una ecuación de
segundo grado
segundo grado
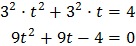
Para llegar a la solución aplicaremos la formula general.
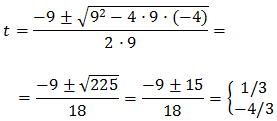
Por tanto, tenemos
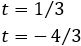
Al deshacer el cambio de variable,
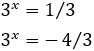
La segunda solución no es posible porque es negativa, pero la primera sí.
a.- ( 1/3 ; si) b.- (-4/3 ; no)
Luego debe cumplirse
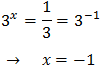
Por tanto, la solución de la ecuación exponencial es:
X = -1
PROPIEDADES
Esto nos permite simplificar las
ecuaciones exponenciales o escribirlas en una forma que facilite su resolución.
Las propiedades de las potencias son las
siguientes:
- Producto (misma base)
Ejemplo:
- Potencia de potencia
Ejemplo:
- Cociente
Ejemplo:
- Exponente Negativo
Ejemplo:
También, en algunos casos hacemos el uso de la formula general:

Ejemplo:
OBJETIVO
El objetivo de este blog, es que a través de ello podamos aprender de una manera mas eficaz y sencilla, sobre las ecuaciones exponenciales.
Aplicando las propiedades que estamos facilitando, seguido de los ejemplos resueltos.Con el fin de compartir y transformar el conocimiento del tema que estamos brindando.
Aplicando las propiedades que estamos facilitando, seguido de los ejemplos resueltos.Con el fin de compartir y transformar el conocimiento del tema que estamos brindando.
INTRODUCCIÓN
- Las funciones exponencial son las que tienen más presencia en los fenómenos
observables, por lo que existen diversidad de situaciones cuyo estudio implica el planteamiento
de ecuaciones exponenciales.
- Se llaman ecuaciones exponenciales a las ecuaciones en las que en algún miembro aparece la
incógnita en una expresión exponencial.
- Inicialmente, como en cualquier ecuación, se trata de encontrar algún valor de "x" que cumpla la
igualdad.
En casos sencillos, eso se puede lograr por simple observación.
- Para conseguir igualdades como la anterior, tendremos que factorizar, expresar los números en forma de potencias, aplicar las propiedades de las potencias y escribir las raíces como potencias. En ocasiones, tendremos que realizar un cambio de variable para transformar la ecuación en una ecuación de primer o de segundo grado e, incluso, de grado mayor.
Suscribirse a:
Comentarios (Atom)











